Linia

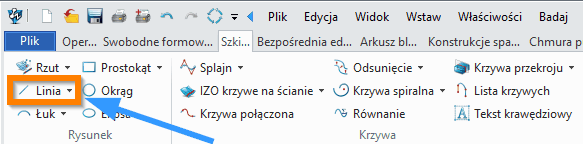
Pozwala na utworznie linii w przestrzeni 3D.
Szkic 3D > Rysunek

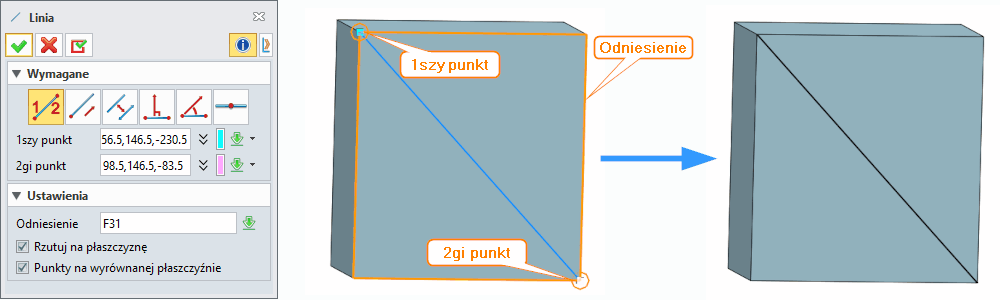
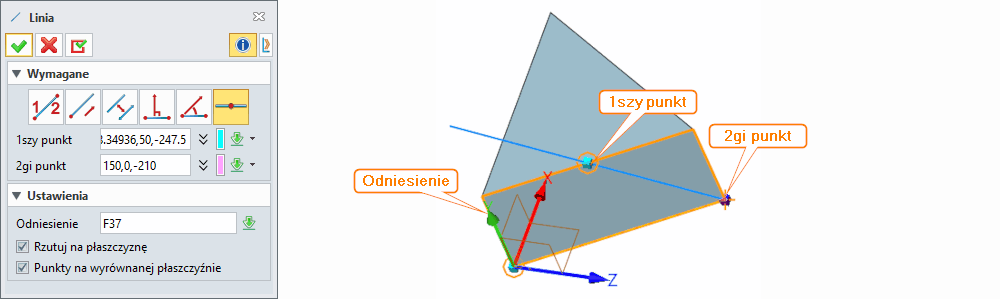
Aby skorzystać z funkcji wymagane jest wybranie opcji:
- 2 punktowa linia.
- Linia wzdłóż kierunku.
- Równoległa linia.
- Prostopadła linia.
- Linia pod kątem.
- Punkt środkowy. 

W przypadku 2 punktowej linii należy wskazać 1szy punkt oraz 2gi punkt. W Ustawieniach możemy posłużyć się płaszczyzną Odniesienia. Może to być płaszczyzna lub płaska powierzchnia (sciana). Gdy korzystamy z Odniesienia, możemy również wykorzystać opcje Rzutuj na płaszczyznę. Nie zaznaczając tej opcji, linia znajdzie się na równoległej płaszczyźnie do wybranej płaszczyzny wraz z punktami.
Punkty na wyrównanej płaszczyźnie umożliwia wstawienie punktów na jednej płaszczyźnie Odniesienia.

Opcje Wyrównaj do płaszczyzny i Rzutuj na płaszczyznę są używane w metodzie rysowania linii za pomocą dwóch punktów. W tym poleceniu, jeśli chcesz wyrównać lub rzutować linię względem płaszczyzny, musisz najpierw wybrać płaszczyznę wyrównania, a dopiero potem dwa punkty.

Linia wzdłóż kierunku

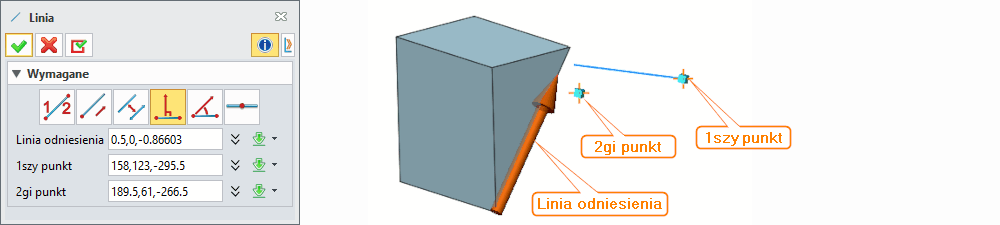
Wybieramy Linię odniesienia a następnie 1szy punkt oraz 2gi punkt.

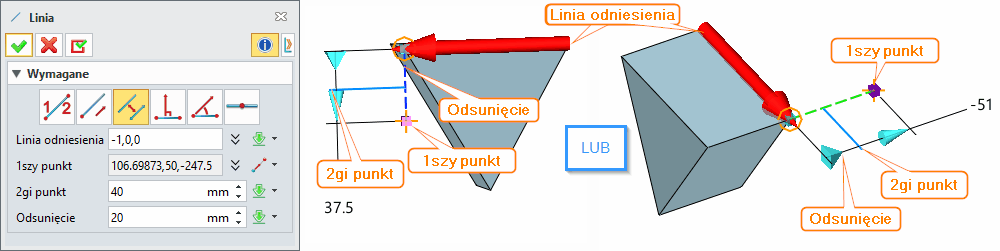
Równoległa linia

Wybieramy Linię odniesienia, a następnie 1szy punkt. Po jego wskazaniu możemy zmodyfikować płaszczyznę, na której będzie znajdować się Linia równoległa. Chwytamy wcześniej zdefiniowany 1szy punkt i przeciągamy go w kierunku płaszczyzny, która nas interesuje. Może być to płaszczyzna powyżej lub poniżej punktu lub po lewej lub prawej stronie punktu Długość linii definiujemy 2gim punktem. Możemy teraz wstawić wartość Odsunięcia od Linii odniesienia.

Prostopadła linia

Wybieramy Linię odniesienia, a następnie 1szy punkt. Wraz z Linią odniesienia definiuje on płaszczyznę, na której będzie tworzona linia prostopadła. 2gi punkt wskazuje jej długość. Jest to odcięcie linii równoległej do Linii odniesienia w przestrzeni 3D. 

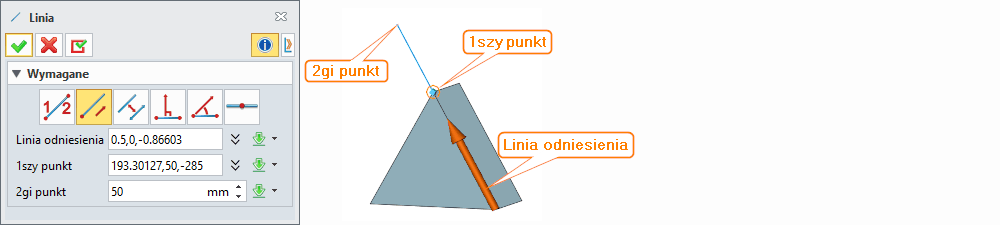
Linia pod kątem

Wybieramy Linię odniesienia, a następnie 1szy punkt. Definiujemy Kąt. Jest on mierzony od punktu wyznaczającego linię równoległą do Linii odniesienia. 2gi punkt definiuje długość Linii pod kątem. 

Punkt środkowy

Wybieramy 1szy punkt oraz 2gi punkt. Możemy posłużyć się jak w pierwszym przypadku płaszczyzną Odniesienia, Rzutowaniem na płaszczyznę oraz Punktami na wyrównanej płaszczyźnie.